Published on: March 4, 2024
Created by Calculator Services Team / Fact-checked by Monjurul Kader
A Channel Capacity Calculator is a tool designed to measure the maximum data transfer rate of a communication channel. It uses the Shannon-Hartley theorem to calculate this rate, taking into account the signal-to-noise ratio (SNR) and the bandwidth of the channel. This calculation is vital for engineers and professionals in telecommunications to optimize data transmission and ensure efficient network performance.
The concept of channel capacity is foundational in the field of information theory and telecommunications. It represents the upper limit on the amount of information that can be reliably transmitted over a communication channel. The Shannon-Hartley theorem, which forms the basis of this calculator, posits that the capacity of a channel increases with its bandwidth and the logarithm of the signal-to-noise ratio. This relationship highlights the balance between available resources and the quality of communication.
Using the Channel Capacity Calculator, users can input the SNR in either linear or decibel (dB) form, along with the bandwidth in various units like Hz, kHz, MHz, or GHz. The calculator then processes these inputs to output the channel capacity in bits per second (bps). This tool is especially useful for designing and analyzing communication systems, allowing for the optimization of bandwidth usage and the improvement of signal quality.
For those interested in maximizing the efficiency of their communication channels or simply learning more about how data transmission capabilities are determined, the detailed article below offers in-depth insights. It covers the theoretical underpinnings of channel capacity, practical applications, and key considerations for using the Channel Capacity Calculator effectively.
See More Useful Calculators:
- Car Wash Profit Calculator
- Candle Cost Calculator
- Cake Delivery Fee Calculator
- Tip Calculator for Nails
- TikTok Gift Points to Money Calculator
- AoS Damage Calculator for Strategic Gameplay
- YTD Monthly Income Calculator
- Bus Rental Cost Calculator
Channel Capacity
The Essence of Channel Capacity in Telecommunications
Channel capacity serves as the backbone of telecommunications, representing the maximum rate at which data can be transmitted over a communication channel without errors. This concept is pivotal for ensuring efficient and reliable data transfer across networks, laying the groundwork for the development and optimization of communication technologies.
The Shannon-Hartley Theorem Unpacked
At the heart of channel capacity calculation lies the Shannon-Hartley theorem. This theorem provides a formula that quantifies the maximum information rate for a particular channel, considering its bandwidth and the signal-to-noise ratio (SNR). It’s a cornerstone principle that guides telecommunications engineers in maximizing data transmission rates.
The Calculation Formula
Breaking Down the Channel Capacity Formula
The channel capacity, C, can be calculated using the formula
The channel capacity, C, can be calculated using the formula:
C = B × log2(1 + S/N)
where C is the channel capacity in bits per second (bps), B is the bandwidth in hertz (Hz), and S/N is the signal-to-noise ratio. This formula encapsulates the relationship between bandwidth, SNR, and the potential data transmission rate.
Key Assumptions of the Shannon-Hartley Theorem
The Role of White Gaussian Noise
The theorem assumes the presence of white Gaussian noise, a type of random noise with a constant power spectral density. This assumption is crucial as it simplifies the calculation by providing a standard noise model, allowing for a more straightforward determination of channel capacity.
Ideal Conditions and Their Implications
The theorem posits an ideal scenario where the only limiting factor is the noise, disregarding other potential impairments like fading or interference. This idealization helps in establishing an upper bound for channel capacity, guiding engineers in understanding the best-case scenario for data transmission rates.
Practical Applications
Enhancing Network Design and Optimization
Understanding channel capacity is vital for network designers and telecommunications engineers. It aids in making informed decisions about bandwidth allocation, signal enhancement, and overall network architecture to achieve optimal performance.
Shaping Telecommunications Strategies
The principles of channel capacity influence strategies for managing data flow, improving signal quality, and reducing errors. These strategies are fundamental in designing robust communication systems that can handle the ever-increasing demand for data transmission.
Example Calculations
Sample SNR Values and Corresponding Channel Capacities
| SNR (dB) | Bandwidth (MHz) | Channel Capacity (Mbps) |
|---|---|---|
| 10 | 5 | 34.86 |
| 20 | 5 | 69.73 |
| 10 | 10 | 69.73 |
| 20 | 10 | 139.45 |
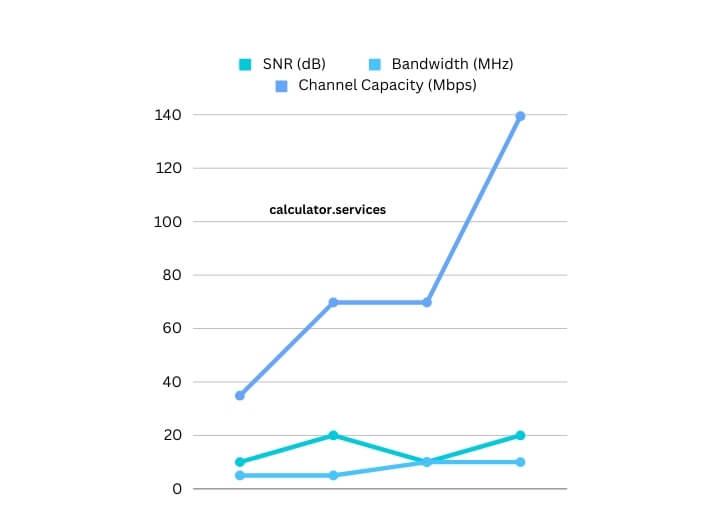
This table illustrates how channel capacity increases with both SNR and bandwidth, showcasing the direct impact of these factors on data transmission rates.
Bandwidth Variations and Channel Capacity Outcomes
| Bandwidth (MHz) | SNR (dB) | Channel Capacity (Mbps) |
|---|---|---|
| 2 | 10 | 13.95 |
| 2 | 20 | 27.89 |
| 5 | 10 | 34.86 |
| 5 | 20 | 69.73 |
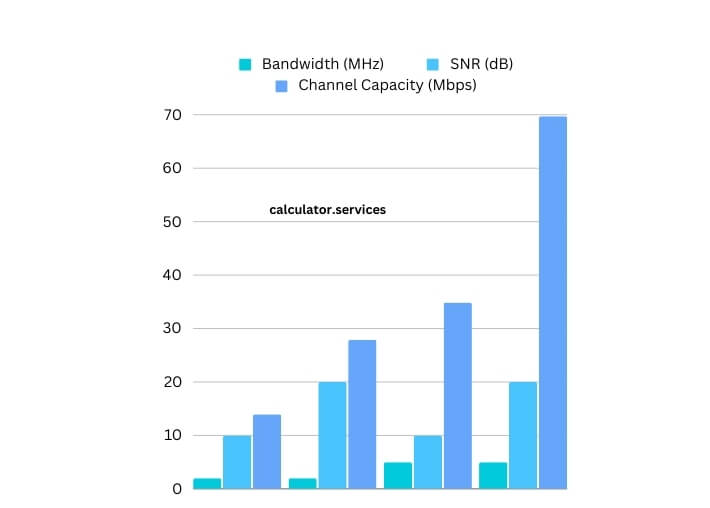
The data presented in this table further emphasizes the relationship between bandwidth, SNR, and channel capacity, highlighting the importance of optimizing both parameters to enhance data transmission capabilities.
Summary
In conclusion, the Channel Capacity Calculator embodies a critical tool for telecommunications, enabling professionals to quantify the maximum data transmission rate under given conditions. By leveraging the Shannon-Hartley theorem, this calculator not only aids in the design and optimization of communication systems but also in strategic decision-making to improve network performance. Through example calculations and practical applications, it’s clear that understanding and applying the principles of channel capacity are essential for advancing telecommunications infrastructure.
