Published on: December 21, 2023
Created by Calculator Services Team / Fact-checked by Monjurul Kader
Bohr Formula Calculator
The Bohr formula calculator is an interactive tool designed to calculate the angular momentum in an atom using Bohr’s theory. It simplifies complex quantum mechanics concepts into an easy-to-use online application.
Niels Bohr, a pioneer in atomic structure and quantum theory, introduced the Bohr model, which explains how electrons orbit the nucleus in atoms. This model is fundamental in the field of quantum mechanics and forms the basis of the Bohr formula. The formula itself is a mathematical representation that calculates the angular momentum of an electron orbiting a nucleus. It is expressed as L = n * H / (2 * pi), where L is the angular momentum, n is the principal quantum number, H is Planck’s constant, and pi is the mathematical constant π.
The Bohr formula calculator is a valuable resource for students, educators, and professionals in physics and chemistry. It allows users to input the principal quantum number and automatically computes the angular momentum. This tool is particularly useful in educational settings, providing a practical application of theoretical concepts. It helps in visualizing and understanding the quantized nature of electron orbits in atoms, a concept that can be challenging to grasp through textbooks alone.
The calculator is designed to be user-friendly, ensuring that even those new to quantum mechanics can easily engage with the tool. It serves as an excellent starting point for those interested in the intricacies of atomic structures and quantum physics. We invite you to read the detailed article below and use the Bohr formula calculator to enhance your understanding of this fascinating aspect of quantum mechanics.

See More Useful Calculators:
- Renin/Aldosterone Ratio Calculator
- AP Physics C E&M Exam: Score Calculator
- Maximize Air Quality with the Air Scrubber Calculator
- Calculate Earth’s Average Speed Relative to the Sun
- Back Vertex Calculator
- Aluminum Coil Weight Calculator
The Bohr Model: A Brief Overview
Historical Context of Bohr’s Theory
Let’s take a trip back to the early 20th century, where Niels Bohr made a groundbreaking leap in atomic physics. Picture a young Bohr, deep in thought, challenging the then-accepted atomic models. His theory was revolutionary, suggesting that electrons orbit the nucleus at fixed distances. This was a game-changer, laying the groundwork for modern quantum mechanics. It’s like Bohr handed us the first piece of a jigsaw puzzle that helped us see the bigger picture of atomic structure.
Key Components of the Bohr Model
Bohr’s model is like the rulebook for the atomic world. It tells us that electrons move in specific orbits, or shells, around the nucleus. Each orbit corresponds to a certain energy level – think of it as a cosmic ladder, where each rung represents a different orbit. The higher the electron climbs, the more energy it needs. This model was a stepping stone, helping us move from classical physics to quantum mechanics.
The Bohr Formula
Mathematical Breakdown of the Formula
Now, let’s get our hands dirty with some math. The Bohr formula, L = n * H / (2 * pi), might look daunting at first, but it’s actually pretty straightforward. Here, L stands for the angular momentum of an electron, n is the principal quantum number (like the address of the electron’s orbit), H is Planck’s constant, and pi, well, that’s our good old mathematical friend, 3.14159… This formula is like a secret code that unlocks the behavior of electrons in their orbits.
Significance in Quantum Mechanics
The Bohr formula isn’t just a random equation; it’s a cornerstone of quantum mechanics. It shows us how quantized the atomic world is. In simpler terms, it tells us that not everything in the atomic realm is continuous – some things, like the electron’s orbit, come in fixed sizes or quantities. It’s like discovering that you can only fill your gas tank in gallons, not continuously.
Practical Application of the Bohr Formula
Common Values in Bohr Calculations
| Principal Quantum Number (n) | Planck’s Constant (H) | Angular Momentum (L) |
| 1 | 6.626 x 10^-34 m^2 kg / s | 1.054 x 10^-34 kg m^2/s |
| 2 | 6.626 x 10^-34 m^2 kg / s | 2.108 x 10^-34 kg m^2/s |
| 3 | 6.626 x 10^-34 m^2 kg / s | 3.162 x 10^-34 kg m^2/s |
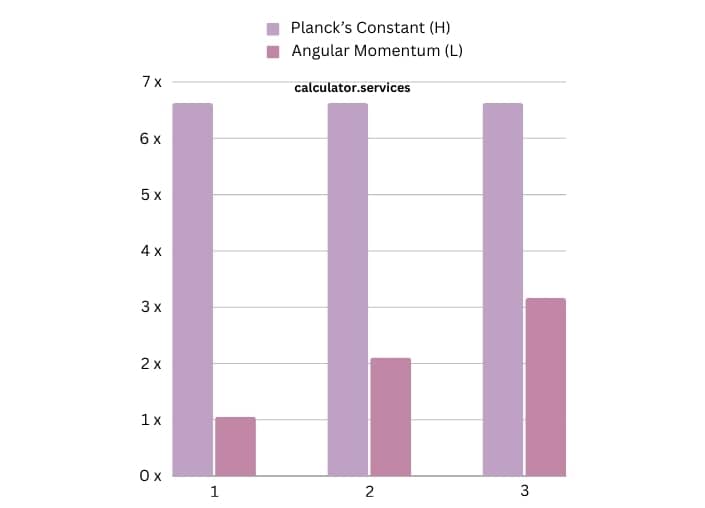
This table shows how changing the principal quantum number affects the angular momentum. It’s like adjusting the volume on your TV – as you go higher, the sound (in our case, the angular momentum) increases.
Real-World Examples in Physics and Chemistry
In the real world, the Bohr formula helps us understand phenomena like atomic spectra – the colors emitted by atoms when they get excited. It’s like each atom has its own unique fingerprint of light, and the Bohr formula helps us read these fingerprints.
The Bohr Formula in Modern Physics
Evolution from Bohr to Quantum Mechanics
Bohr’s formula was just the beginning. It opened doors to the vast, intricate world of quantum mechanics. Think of it as the first step on a long journey – a journey that has led us to understand the quantum nature of reality. From the tiny particles that make up our universe to the complex behaviors of atoms, Bohr’s insights were the spark that ignited a scientific revolution.
Current Relevance and Applications
Even today, the Bohr formula is more than just a historical footnote. It’s actively used in fields like spectroscopy, where scientists study the interaction between matter and electromagnetic radiation. It’s like having a Swiss Army knife in the world of atomic physics – versatile and still very much relevant.
Using the Bohr Formula Calculator
Step-by-Step Guide
Using the Bohr formula calculator is a breeze. You just plug in the principal quantum number, and voilà, it gives you the angular momentum. It’s like using a GPS – you input your destination (the principal quantum number) and get the route (angular momentum).
Sample Calculations and Results
| Principal Quantum Number (n) | Calculated Angular Momentum (L) |
| 4 | 4.216 x 10^-34 kg m^2/s |
| 5 | 5.270 x 10^-34 kg m^2/s |
| 6 | 6.324 x 10^-34 kg m^2/s |
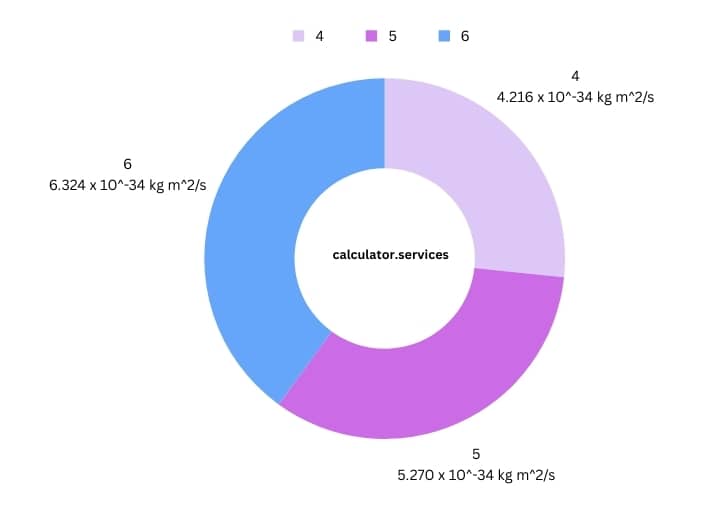
This table gives you a taste of what the calculator can do. It’s like seeing the formula come to life, turning abstract numbers into tangible results.
In a nutshell, the Bohr formula calculator is not just a tool; it’s a bridge connecting us to the quantum world. It takes the complex, often intimidating world of quantum mechanics and makes it accessible. Whether you’re a student, a teacher, or just a curious mind, this calculator is your gateway to understanding one of the fundamental aspects of physics. It’s like having a quantum physicist in your pocket, ready to demystify the mysteries of the atom.
